Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций.

Первообразная и неопределенный интеграл

Первообразная F(x) от функции f(x) - это такая функция, производная которой равна f(x) :
F′(x) = f(x), x ∈ Δ ,
где Δ - промежуток, на котором выполняется данное уравнение.

Совокупность всех первообразных называется неопределенным интегралом:
,
где C - постоянная, не зависящая от переменной x .

Основные формулы и методы интегрирования

Таблица интегралов

Конечная цель вычисления неопределенных интегралов - путем преобразований, привести заданный интеграл к выражению, содержащему простейшие или табличные интегралы.
См. Таблица интегралов >>>

Правило интегрирования суммы (разности)

Вынесение постоянной за знак интеграла

Пусть c - постоянная, не зависящая от x . Тогда ее можно вынести за знак интеграла:

Замена переменной

Пусть x - функция от переменной t , x = φ(t) , тогда
.
Или наоборот, t = φ(x) ,
.

С помощью замены переменной можно не только вычислить простые интегралы, но и упростить вычисление более сложных.

Правило интегрирования по частям

Интегрирование дробей (рациональных функций)

Введем обозначение. Пусть P k (x), Q m (x), R n (x) обозначают многочлены степеней k, m, n , соответственно, относительно переменной x .

Рассмотрим интеграл, состоящий из дроби многочленов (так называемая рациональная функция):

Если k ≥ n , то сначала нужно выделить целую часть дроби:
.
Интеграл от многочлена S k-n (x) вычисляется по таблице интегралов.

Остается интеграл:
, где m < n .
Для его вычисления, подынтегральное выражение нужно разложить на простейшие дроби.

Для этого нужно найти корни уравнения:
Q n (x) = 0 .
Используя полученные корни, нужно представить знаменатель в виде произведения сомножителей:
Q n (x) = s (x-a) n a (x-b) n b ... (x 2 +ex+f) n e (x 2 +gx+k) n g ... .
Здесь s - коэффициент при x n , x 2 + ex + f > 0 , x 2 + gx + k > 0 , ... .

После этого разложить дробь на простейшие:

Интегрируя, получаем выражение, состоящее из более простых интегралов.
Интегралы вида

приводятся к табличным подстановкой t = x - a .

Рассмотрим интеграл:

Преобразуем числитель:
.
Подставляя в подынтегральное выражение, получаем выражение, в которое входят два интеграла:
,
.
Первый, подстановкой t = x 2 + ex + f приводится к табличному.
Второй, по формуле приведения:

приводится к интегралу

Приведем его знаменатель к сумме квадратов:
.
Тогда подстановкой , интеграл

также приводится к табличному.

Интегрирование иррациональных функций

Введем обозначение. Пусть R(u 1 , u 2 , ... , u n) означает рациональную функцию от переменных u 1 , u 2 , ... , u n . То есть
,
где P, Q - многочлены от переменных u 1 , u 2 , ... , u n .

Дробно-линейная иррациональность

Рассмотрим интегралы вида:
,
где - рациональные числа, m 1 , n 1 , ..., m s , n s - целые числа.
Пусть n - общий знаменатель чисел r 1 , ..., r s .
Тогда интеграл сводится к интегралу от рациональных функций подстановкой:
.

Интегралы от дифференциальных биномов

Рассмотрим интеграл:
,
где m, n, p - рациональные числа, a, b - действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.

1) Если p - целое. Подстановка x = t N , где N - общий знаменатель дробей m и n .
2) Если - целое. Подстановка a x n + b = t M , где M - знаменатель числа p .
3) Если - целое. Подстановка a + b x - n = t M , где M - знаменатель числа p .

Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.

В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям m и p . Это можно сделать с помощью формул приведения:
;
.

Интегралы, содержащие квадратный корень из квадратного трехчлена

Здесь мы рассматриваем интегралы вида:
,

Подстановки Эйлера

Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0 ;
, при c > 0 ;
, где x 1 - корень уравнения a x 2 + b x + c = 0 . Если это уравнение имеет действительные корни.

Тригонометрические и гиперболические подстановки

Прямые методы

В большинстве случаев, подстановки Эйлера приводят к более длинным вычислениям, чем прямые методы. С помощью прямых методов интеграл приводится к одному из перечисленных ниже видов.

I тип

Интеграл вида:
,
где P n (x) - многочлен степени n .

Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:

Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты A i .

II тип

Интеграл вида:
,
где P m (x) - многочлен степени m .

Подстановкой t = (x - α) -1 этот интеграл приводится к предыдущему типу. Если m ≥ n , то у дроби следует выделить целую часть.

III тип

Третий и наиболее сложный тип:
.

Здесь нужно сделать подстановку:
.
После чего интеграл примет вид:
.
Далее, постоянные α, β нужно выбрать такими, чтобы коэффициенты при t обратились в нуль:
B = 0, B 1 = 0 .
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
z 2 = A 1 t 2 + C 1 ;
y 2 = A 1 + C 1 t -2 .

Общий случай

Интегрирование трансцендентных (тригонометрических и показательных) функций

Заранее отметим, что те методы, которые применимы для тригонометрических функций, также применимы и для гиперболических функций. По этой причине мы не будем рассматривать интегрирование гиперболических функций отдельно.

Интегрирование рациональных тригонометрических функций от cos x и sin x

Рассмотрим интегралы от тригонометрических функций вида:
,
где R - рациональная функция. Сюда также могут входить тангенсы и котангенсы, которые следует преобразовать через синусы и косинусы.

При интегрировании таких функций полезно иметь в виду три правила:
1) если R(cos x, sin x) умножается на -1 от перемены знака перед одной из величин cos x или sin x , то полезно другую из них обозначить через t .
2) если R(cos x, sin x) не меняется от перемены знака одновременно перед cos x и sin x , то полезно положить tg x = t или ctg x = t .
3) подстановка во всех случаях приводит к интегралу от рациональной дроби. К сожалению, эта подстановка приводит к более длинным вычислениям чем предыдущие, если они применимы.

Произведение степенных функций от cos x и sin x

Рассмотрим интегралы вида:

Если m и n - рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.

Если m и n - целые числа, то интегралы вычисляются интегрированием по частям. При этом получаются следующие формулы приведения:

;
;
;
.

Интегрирование по частям

Применение формулы Эйлера

Если подынтегральное выражение линейно относительно одной из функций
cos ax или sin ax , то удобно применить формулу Эйлера:
e iax = cos ax + isin ax (где i 2 = -1 ),
заменив эту функцию на e iax и выделив действительную (при замене cos ax ) или мнимую часть (при замене sin ax ) из полученного результата.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на оптимизацию.

Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача - задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.

Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти закон движения.
Решение. Пусть s = s(t) - искомый закон движения. Известно, что s"(t) = v(t). Значит, для решения задачи нужно подобрать функцию s = s(t), производная которой равна gt. Нетрудно догадаться, что \(s(t) = \frac{gt^2}{2} \). В самом деле
\(s"(t) = \left(\frac{gt^2}{2} \right)" = \frac{g}{2}(t^2)" = \frac{g}{2} \cdot 2t = gt \)
Ответ: \(s(t) = \frac{gt^2}{2} \)

Сразу заметим, что пример решен верно, но неполно. Мы получили \(s(t) = \frac{gt^2}{2} \). На самом деле задача имеет бесконечно много решений: любая функция вида \(s(t) = \frac{gt^2}{2} + C \), где C - произвольная константа, может служить законом движения, поскольку \(\left(\frac{gt^2}{2} +C \right)" = gt \)

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s 0 , то из равенства s(t) = (gt 2)/2 + C получаем: s(0) = 0 + С, т. е. C = s 0 . Теперь закон движения определен однозначно: s(t) = (gt 2)/2 + s 0 .

В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например: возведение в квадрат (х 2) и извлечение квадратного корня (\(\sqrt{x} \)), синус (sin x) и арксинус (arcsin x) и т. д. Процесс нахождения производной по заданной функции называют дифференцированием , а обратную операцию, т. е. процесс нахождения функции по заданной производной, - интегрированием .

Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у" = f"(x). Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции у" = f"(x), первичный образ, или первообразная.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для \(x \in X \) выполняется равенство F"(x) = f(x)

На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).

Приведем примеры.
1) Функция у = х 2 является первообразной для функции у = 2х, поскольку для любого х справедливо равенство (x 2)" = 2х
2) Функция у = х 3 является первообразной для функции у = 3х 2 , поскольку для любого х справедливо равенство (x 3)" = 3х 2
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство (sin(x))" = cos(x)

При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.

Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.

Правило 1. Первообразная суммы равна сумме первообразных.

Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.

Правило 2. Если F(x) - первообразная для f(x), то kF(x) - первообразная для kf(x).

Теорема 1. Если y = F(x) - первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция \(y=\frac{1}{k}F(kx+m) \)

Теорема 2. Если y = F(x) - первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид y = F(x) + C.

Методы интегрирования

Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл \(\textstyle \int F(x)dx \). Сделаем подстановку \(x= \varphi(t) \) где \(\varphi(t) \) - функция, имеющая непрерывную производную.
Тогда \(dx = \varphi " (t) \cdot dt \) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)

Интегрирование выражений вида \(\textstyle \int \sin^n x \cos^m x dx \)

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям - применение следующей формулы для интегрирования:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
или:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)

Таблица неопределённых интегралов (первообразных) некоторых функций

Найти неопределённый интеграл (множество первообразных или "антипроизводных") означает восстановить функцию по известной производной этой функции. Восстановленное множество первообразных F (x ) + С для функции f (x ) учитывает константу интегрирования C . По скорости перемещения материальной точки (производной) может быть восстановлен закон движения этой точки (первообразная); по ускорению движения точки - её скорость и закон движения. Как видно, интегрирование - широкое поле для деятельности Шерлоков Холмсов от физики. Да и в экономике многие понятия представляются через функции и их производные и поэтому, например, можно по производительности труда в определённый момент времени (производной) восстановить объём продукции, выпущенный в соответствующее время.

Чтобы найти неопределённый интеграл, требуется довольно небольшое количество основных формул интегрирования. Но процесс его нахождения значительно труднее, чем одно лишь применение этих формул. Вся сложность относится не к интегрированию, а к приведению интегрируемого выражения к такому виду, который даёт возможность найти неопределённый интеграл по упомянутым выше основным формулам. Это означает, что для начала практики интегрирования нужно активизировать полученные в средней школе навыки преобразования выражений.

Учиться находить интегралы будем, пользуясь свойствами и таблицей неопределённых интегралов из урока об основных понятиях этой темы (откроется в новом окне).

Существует несколько методов нахождения интеграла, из которых метод замены переменной и метод интегрирования по частям - обязательный джентльменский набор каждого, кто успешно сдал высшую математику. Однако начинать осваивать интегрирование полезнее и приятнее с применением метода разложения, основанном на следующих двух теоремах о свойствах неопределённого интеграла, которые для удобства повторим здесь.

Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

(2)

Кроме того, в интегрировании может пригодиться следующее правило: если выражение подынтегральной функции содержит постоянный множитель, то выражение первообразной домножается на число, обратное постоянному множителю, то есть

(3)

Поскольку этот урок - вводный в решение задач интегрирования, важно отметить две вещи, которые либо уже на самом начальном этапе, либо несколько позже могут вас удивить. Удивление связано с тем фактом, что интегрирование - операция обратная дифференцированию и неопределённый интеграл можно справедливо называть "антипроизводной".

Первая вещь, которой не следует удивляться при интегрировании. В таблице интегралов существуют формулы, которые не имеют аналогов среди формул таблицы производной . Это следующие формулы:

Однако можно убедиться в том, что производные выражений, стоящих в правых частях этих формул, совпадают с соответствующими подынтегральными функциями.

Вторая вещь, которой не следует удивляться при интегрировании . Хотя производная любой элементарной функции представляет собой также элементарную функцию, неопределённые интегралы от некоторых элементарных функций уже не являются элементарными функциями . Примерами таких интегралов могут быть следующие:

Для выработки техники интегрирования пригодятся следующие навыки: сокращение дробей, деление многочлена в числителе дроби на одночлен в знаменателе (для получения суммы неопределённых интегралов), преобразование корней в степени, умножение одночлена на многочлен, возведение в степень. Эти навыки нужны для преобразований подынтегрального выражения, в результате которых должна получиться сумма интегралов, присутствующих в таблице интегралов.

Находим неопределённые интегралы вместе

Пример 1. Найти неопределённый интеграл

.

Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл 21 (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:

Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:

.

Пример 2. Найти неопределённый интеграл

Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:

Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:

.

Сокращаем получившиеся дроби и перед нами конечный ответ:

Пример 3. Найти неопределённый интеграл

Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:

Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда

объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.

Пример 4. Найти неопределённый интеграл

Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:

.

Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:

Продолжаем находить неопределённые интегралы вместе

Пример 7. Найти неопределённый интеграл

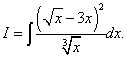
Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов.

А можно ли под знак дифференциала подводить нелинейную функцию? Да, если подынтегральное выражение представляет собой произведение двух множителей: один множитель — сложная функция от какой-то нелинейной функции, а другой множитель есть производная от этой нелинейной функции. Рассмотрим сказанное на примерах.

Найти неопределенные интегралы.

Пример 1 . ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6 + C.

Что представляет собой данное подынтегральное выражение? Произведение степенной функции от (х 2 + х + 2) и множителя (2х + 1), который равен производной от основания степени: (х 2 + х + 2)" = 2х + 1.

Это и позволило нам подвести (2х + 1) под знак дифференциала:

∫u 5 du=u 6 : 6+ C. (Формула 1). )

Проверка. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)′=1/6 · 6 (x 2 + x + 2) 5 · (x 2 + x + 2)" =

=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1)(x 2 + x + 2) 5 = f (x).

Пример 2. ∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6 + C

И чем этот пример отличается от примера 1? Да ничем! Та же пятая степень с основанием (х 3 – х 2 + 3х + 1) умножается на трехчлен (3х 2 – 2х + 3), который является производной основания степени: (х 3 – х 2 + 3х + 1)" = 3х 2 – 2х + 3. Это основание степени мы и подвели под знак дифференциала, от чего значение подынтегрального выражения не изменилось, а затем применили ту же формулу 1). (Интегралы )

Пример 3.

Здесь производная от (2х 3 – 3х) даст (6х 2 – 3), а у нас

имеется (12х 2 – 6), то есть выражение в 2 раза большее, значит, подведем (2х 3 – 3х) под знак дифференциала, а перед интегралом поставим множитель 2 . Применим формулу 2) (лист ).

Вот что получится:

Сделаем проверку, учитывая, что:

Примеры. Найти неопределенные интегралы.

1. ∫(6х+5) 3 dx. Как будем решать? Смотрим в лист и рассуждаем примерно так: подынтегральная функция представляет собой степень, а у нас есть формула для интеграла степени (формула 1) ), но в ней основание степени u и переменная интегрирования тоже u.

А у нас переменная интегрирования х , а основание степени (6х+5) . Сделаем замену переменной интегрирования: вместо dx запишем d (6х+5). Что изменилось? Так как, то, что стоит после знака дифференциала d, по умолчанию, дифференцируется,

то d (6x+5)=6dx, т.е. при замене переменной х на переменную (6х+5) подынтегральная функция возросла в 6 раз, поэтому перед знаком интеграла ставим множитель 1/6. Записать эти рассуждения можно так:

Итак, мы решили этот пример введением новой переменной (переменную х заменили на переменную 6х+5). А куда записали новую переменную (6х+5)? Под знак дифференциала. Поэтому, данный метод введения новой переменной часто называют методом (или способом) подведения (новой переменной) под знак дифференциала .

Во втором примере мы вначале получили степень с отрицательным показателем, а затем подвели под знак дифференциала (7х-2) и использовали формулу интеграла степени 1) (Интегралы ).

Разберем решение примера 3.

Перед интегралом стоит коэффициент 1/5. Почему? Так как d (5x-2)=5dx, то, подведя под знак дифференциала функцию u=5x-2, мы увеличили подынтегральное выражение в 5 раз, поэтому, чтобы значение данного выражения не изменилось — надо было разделить на 5, т.е. умножить на 1/5. Далее, была использована формула 2) (Интегралы) .

Все простейшие формулы интегралов будут иметь вид:

∫f (x) dx=F (x)+C , причем, должно выполняться равенство:

(F (x)+C)"=f (x).

Формулы интегрирования можно получить обращением соответствующих формул дифференцирования.

Действительно,

Показатель степени n может быть и дробным. Часто приходится находить неопределенный интеграл от функции у=√х. Вычислим интеграл от функции f (x)=√x, используя формулу 1) .

Запишем этот пример в виде формулы 2) .

Так как (х+С)"=1, то ∫dx=x+C.

3) ∫dx=x+C.

Заменяя 1/х² на х -2 , вычислим интеграл от 1/х².

А можно было получить этот ответ обращением известной формулы дифференцирования:

Запишем наши рассуждения в виде формулы 4).

Умножив обе части полученного равенства на 2, получим формулу 5).

Найдем интегралы от основных тригонометрических функций, зная их производные: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Получаем формулы интегрирования 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

После изучения показательной и логарифмической функций, добавим еще несколько формул.

Основные свойства неопределенного интеграла.

I. Производная неопределенного интеграла равна подынтегральной функции.

(∫f (x) dx)"=f (x).

II. Дифференциал неопределенного интеграла равен подынтегральному выражению.

d∫f (x) dx=f (x) dx.

III. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С.

∫dF (x)=F (x)+C или ∫F"(x) dx=F (x)+C.

Обратите внимание: в I, II и III свойствах знаки дифференциала и интеграла (интеграла и дифференциала) «съедают» друг друга!

IV. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла.

∫kf (x) dx=k·∫f (x) dx, где k - постоянная величина, не равная нулю.

V. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. Если F (x) есть первообразная для f (x), а k и b — постоянные величины, причем, k ≠0, то (1/k)·F (kx+b) есть первообразная для f (kx+b). Действительно, по правилу вычисления производной сложной функции имеем:

Можно записать:

Для каждого математического действия существует обратное ему действие. Для действия дифференцирования (нахождения производных функций) тоже существует обратное действие — интегрирование. Посредством интегрирования находят (восстанавливают) функцию по заданной ее производной или дифференциалу. Найденную функцию называют первообразной .

Определение. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство: F′(x)=f (x) .

Примеры. Найти первообразные для функций: 1) f (x)=2x; 2) f (x)=3cos3x.

1) Так как (х²)′=2х, то, по определению, функция F (x)=x² будет являться первообразной для функции f (x)=2x.

2) (sin3x)′=3cos3x. Если обозначить f (x)=3cos3x и F (x)=sin3x, то, по определению первообразной, имеем: F′(x)=f (x), и, значит, F (x)=sin3x является первообразной для f (x)=3cos3x.

Заметим, что и (sin3x+5 )′=3cos3x , и (sin3x-8,2 )′=3cos3x , ... в общем виде можно записать: (sin3x+С )′=3cos3x , где С — некоторая постоянная величина. Эти примеры говорят о неоднозначности действия интегрирования, в отличие от действия дифференцирования, когда у любой дифференцируемой функции существует единственная производная.

Определение. Если функция F (x) является первообразной для функции f (x) на некотором промежутке, то множество всех первообразных этой функции имеет вид:

F (x)+C , где С — любое действительное число.

Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом ∫ (знак интеграла). Записывают: ∫f (x) dx=F (x)+C .

Выражение ∫f (x) dx читают: «интеграл эф от икс по дэ икс».

f (x) dx — подынтегральное выражение,

f (x) — подынтегральная функция,

х — переменная интегрирования.

F (x) — первообразная для функции f (x) ,

С — некоторая постоянная величина.

Теперь рассмотренные примеры можно записать так:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Что же означает знак d?

d — знак дифференциала — имеет двойное назначение: во-первых, этот знак отделяет подынтегральную функцию от переменной интегрирования; во-вторых, все, что стоит после этого знака диференцируется по умолчанию и умножается на подынтегральную функцию.

Примеры. Найти интегралы: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) После значка дифференциала d стоит х х , а р

∫ 2хрdx=рх²+С. Сравните с примером 1).

Сделаем проверку. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) После значка дифференциала d стоит р . Значит, переменная интегрирования р , а множитель х следует считать некоторой постоянной величиной.

∫ 2хрdр=р²х+С. Сравните с примерами 1) и 3).

Сделаем проверку. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Страница 1 из 1 1

Неопределенный интеграл.
Подробные примеры решений

На данном уроке мы начнём изучение темы Неопределенный интеграл , а также подробно разберем примеры решений простейших (и не совсем) интегралов. В этой статье я ограничусь минимумом теории , и сейчас наша задача – научиться решать интегралы.

Что нужно знать для успешного освоения материала? Для того чтобы справиться с интегральным исчислением Вам необходимо уметь находить производные, минимум, на среднем уровне. Поэтому, если материал запущен, то рекомендую сначала внимательно ознакомиться с уроками Как найти производную? и Производная сложной функции . Не лишним опытом будет, если у Вас за плечами несколько десятков (лучше – сотня) самостоятельно найденных производных. По-крайне мере, Вас не должны ставить в тупик задания на дифференцирование простейших и наиболее распространенных функций. Казалось бы, при чем здесь вообще производные, если речь в статье пойдет об интегралах?! А дело вот в чем. Дело в том, что нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия , как, например, сложение/вычитание или умножение/деление. Таким образом, без навыка (+ какого-никакого опыта) нахождения производных, к сожалению, дальше не продвинуться.

В этой связи нам потребуются следующие методические материалы: Таблица производных и Таблица интегралов . Справочные пособия можно открыть, закачать или распечатать на странице Математические формулы и таблицы .

В чем сложность изучения неопределенных интегралов? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно четкий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приемов интегрирования. И, если способ интегрирования изначально подобран неверно (т.е. Вы не знаете, как решать), то интеграл можно «колоть» буквально сутками, как самый настоящий ребус, пытаясь приметить различные приемы и ухищрения. Некоторым даже нравится. Между прочим, это не шутка, мне довольно часто приходилось слышать от студентов мнение вроде «У меня никогда не было интереса решить предел или производную, но вот интегралы – совсем другое дело, это увлекательно, всегда есть желание «взломать» сложный интеграл». Стоп. Хватит чёрного юмора, переходим к этим самым неопределенным интегралам.

Коль скоро способов решения существует очень много, то с чего же начать изучение неопределенных интегралов чайнику? В интегральном исчислении существуют, на мой взгляд, три столпа или своеобразная «ось», вокруг которой вращается всё остальное. В первую очередь следует хорошо разобраться в простейших интегралах (эта статья). Потом нужно детально проработать урок . ЭТО ВАЖНЕЙШИЙ ПРИЁМ! Может быть, даже самая важная статья из всех моих статей, посвященных интегралам. И, в-третьих, обязательно следует ознакомиться с методом интегрирования по частям , поскольку с помощью него интегрируется обширный класс функций. Если Вы освоите хотя бы эти три урока, то уже «не два». Вам могут «простить» незнание интегралов от тригонометрических функций , интегралов от дробей , интегралов от дробно-рациональных функций , интегралов от иррациональных функций (корней) , но вот если «сесть в лужу» на методе замены или методе интегрирования по частям – то это будет очень и очень скверно.

В Рунете сейчас весьма распространены демотиваторы. В контексте изучения интегралов, наоборот, просто необходим МОТИВАТОР . Как в том анекдоте про Василия Ивановича, который и Петьку мотивировал, и Аньку мотивировал. Уважаемые лентяи, халявщики и другие нормальные студенты, обязательно прочитайте нижеследующее. Знания и навыки по неопределенному интегралу потребуются в дальнейшей учебе, в частности, при изучении определенного интеграла , несобственных интегралов , дифференциальных уравнений на 2 курсе. Необходимость взять интеграл возникает даже в теории вероятностей ! Таким образом, без интегралов путь на летнюю сессию и 2 курс БУДЕТ РЕАЛЬНО ЗАКРЫТ . Я серьезно. Вывод таков. Чем больше интегралов различных типов вы прорешаете, тем легче будет дальнейшая жизнь . Да, это займет довольно много времени, да, порой, не хочется, да, иногда «да фиг с ним, с этим интегралом, авось не попадется». Но, воодушевлять и греть душу должна следующая мысль, ваши усилия окупятся сполна! Вы будете, как орехи щелкать дифференциальные уравнения и легко расправляться с интегралами, которые встретятся в других разделах высшей математики. Качественно разобравшись с неопределенным интегралом, ВЫ ФАКТИЧЕСКИ ОСВАИВАЕТЕ ЕЩЕ НЕСКОЛЬКО РАЗДЕЛОВ ВЫШКИ .

И поэтому я просто не мог не создать интенсивный курс по технике интегрирования, который получился на удивление коротким – желающие могут воспользоваться pdf-книгой и подготовиться ОЧЕНЬ быстро. Но материалы сайта ни в коем случае не хуже!

Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Нетрудно заметить, что любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:

Сразу разбираемся в обозначениях и терминах:

– значок интеграла.

– подынтегральная функция (пишется с буквой «ы»).

– значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

– подынтегральное выражение или «начинка» интеграла.

– первообразная функция .

– множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа .

Решить интеграл – это значит найти определенную функцию , пользуясь некоторыми правилами, приемами и таблицей .

Еще раз посмотрим на запись:

Посмотрим в таблицу интегралов.

Что происходит? Левые части у нас превращаются в другие функции: .

Упростим наше определение.

Решить неопределенный интеграл – это значит ПРЕВРАТИТЬ его в определенную функцию , пользуясь некоторыми правилами, приемами и таблицей .

Возьмем, например, табличный интеграл . Что произошло? превратился в функцию .

Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл , первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае совсем не обязательно понимать, почему интеграл превращается именно в . Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.

Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно , справедливо следующее :

Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция .

Вернемся к тому же табличному интегралу .

Убедимся в справедливости данной формулы. Берем производную от правой части:

– исходная подынтегральная функция.

Вот, кстати, стало понятнее, почему к функции всегда приписывается константа . При дифференцировании константа всегда превращается в ноль.

Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере , , , и т. д. – все эти функции являются решением интеграла . Решений бесконечно много, поэтому записывают коротко:

Таким образом, любой неопределенный интеграл достаточно легко проверить (в отличие от производных, где хорошую стопудовую проверку можно осуществить разве что с помощью математических программ). Это некоторая компенсация за большое количество интегралов разных видов.

Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной,
с двух правил интегрирования, которые также называют свойствами линейности неопределенного интеграла:

– постоянный множитель можно (и нужно) вынести за знак интеграла.

– интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.

Как видите, правила, в принципе, такие же, как и для производных.

Пример 1

Решение: Удобнее переписать его на бумагу.

(1) Применяем правило . Не забываем записать значок дифференциала под каждым интегралом. Почему под каждым? – это полноценный множитель , если расписывать решение совсем детально, то первый шаг следует записать так:

(2) Согласно правилу , выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом – это константа, её также выносим.
Кроме того, на данном шаге готовим корни и степени для интегрирования. Точно так же, как и при дифференцировании, корни надо представить в виде . Корни и степени, которые располагаются в знаменателе – перенести вверх.

! Примечание: в отличие от производных, корни в интегралах далеко не всегда следует приводить к виду , а степени переносить вверх. Например, – это готовый табличный интеграл, и всякие китайские хитрости вроде совершенно не нужны. Аналогично: – тоже табличный интеграл, нет никакого смысла представлять дробь в виде . Внимательно изучите таблицу!

(3) Все интегралы у нас табличные. Осуществляем превращение с помощью таблицы, используя формулы: , и .
Особое внимание обращаю на формулу интегрирования степенной функции , она встречается очень часто, ее лучше запомнить. Следует отметить, что табличный интеграл – частный случай этой же формулы: .
Константу достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла) .
(4) Записываем полученный результат в более компактном виде, все степени вида снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.

Проверка. Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:

Получена исходная подынтегральная функция , значит, интеграл найден правильно. От чего плясали, к тому и вернулись. Знаете, очень хорошо, когда история с интегралом заканчивается именно так.

Время от времени встречается немного другой подход к проверке неопределенного интеграла, от ответа берется не производная, а дифференциал :

Кто с первого семестра понял, тот понял, но сейчас нам важны не теоретические тонкости, а важно то, что с этим дифференциалом дальше делать. Его необходимо раскрыть, и с формально-технической точки зрения – это почти то же самое, что найти производную. Дифференциал раскрывается следующим образом: значок убираем, справа над скобкой ставим штрих, в конце выражения приписываем множитель :

Получено исходное подынтегральное выражение , значит, интеграл найден правильно.

Второй способ проверки мне нравится меньше, так как приходится дополнительно рисовать большие скобки и тащить значок дифференциала до конца проверки. Хотя он корректнее или «солиднее» что ли.

На самом деле я вообще мог умолчать о втором способе проверки. Дело не в способе, а в том, что мы научились раскрывать дифференциал. Еще раз.

Дифференциал раскрывается следующим образом :

1) значок убираем;
2) справа над скобкой ставим штрих (обозначение производной);
3) в конце выражения приписываем множитель .

Например:

Запомните это. Рассмотренный приём потребуется нам очень скоро.

Пример 2

Найти неопределенный интеграл. Выполнить проверку.

Когда мы находим неопределенный интеграл, то ВСЕГДА стараемся сделать проверку , тем более, для этого есть прекрасная возможность. Далеко не все типы задач в высшей математике является подарком с этой точки зрения. Неважно, что часто в контрольных заданиях проверки не требуется, её никто, и ничто не мешает провести на черновике. Исключение можно сделать лишь тогда, когда не хватает времени (например, на зачете, экзамене). Лично я всегда проверяю интегралы, а отсутствие проверки считаю халтурой и некачественно выполненным заданием.

Пример 3

Найти неопределенный интеграл. Выполнить проверку.

Решение: Анализируя интеграл, мы видим, что у нас произведение двух функций, да еще и возведение в степень целого выражения. К сожалению, на поприще интегральной битвы нет хороших и удобных формул для интегрирования произведения и частного , .

А поэтому, когда дано произведение или частное, всегда имеет смысл посмотреть, а нельзя ли преобразовать подынтегральную функцию в сумму?

Рассматриваемый пример – тот случай, когда можно. Сначала я приведу полное решение, комментарии будут ниже.

(1) Используем старую-добрую формулу квадрата суммы , избавляясь от степени.

(2) Вносим в скобку, избавляясь от произведения.

Пример 4

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Пример 5

Найти неопределенный интеграл. Выполнить проверку.

В данном примере подынтегральная функция представляет собой дробь. Когда мы видим в подынтегральном выражении дробь, то первой мыслью должен быть вопрос: А нельзя ли как-нибудь от этой дроби избавиться, или хотя бы её упростить?

Замечаем, что в знаменателе находится одинокий корень из «икс». Один в поле – не воин, а значит, можно почленно разделить числитель на знаменатель:

Действия с дробными степенями я не комментирую, так как о них неоднократно шла речь в статьях о производной функции. Если Вас все-таки ставит в тупик такой пример, как , и ни в какую не получается правильный ответ , то рекомендую обратиться к школьным учебникам. В высшей математике дроби и действия с ними встречаются на каждом шагу.

Также обратите внимание, что в решении пропущен один шаг, а именно, применение правил , . Обычно уже при начальном опыте решения интегралов данные свойства считают само собой разумеющимися и не расписывают подробно.

Пример 6

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

В общем случае с дробями в интегралах не всё так просто, дополнительный материал по интегрированию дробей некоторых видов можно найти в статье Интегрирование некоторых дробей .

! Но, прежде чем перейти к вышеуказанной статье, необходимо ознакомиться с уроком Метод замены в неопределенном интеграле . Дело в том, что подведение функции под дифференциал или метод замены переменной является ключевым моментом в изучении темы, поскольку встречается не только «в чистых заданиях на метод замены», но и во многих других разновидностях интегралов.

Очень хотелось включить еще несколько примеров в данный урок, но вот сижу сейчас, печатаю этот текст в Вёрде и замечаю, что статья уже выросла до приличных размеров.
А поэтому вводный курс интегралов для чайников подошел к концу.

Желаю успехов!

Решения и ответы:

Пример 2: Решение :

Пример 4: Решение :

В данном примере мы использовали формулу сокращенного умножения

Пример 6: Решение :

Я выполнил проверку, а Вы? ;)