Найти неопределённый интеграл (множество первообразных или "антипроизводных") означает восстановить функцию по известной производной этой функции. Восстановленное множество первообразных F (x ) + С для функции f (x ) учитывает константу интегрирования C . По скорости перемещения материальной точки (производной) может быть восстановлен закон движения этой точки (первообразная); по ускорению движения точки - её скорость и закон движения. Как видно, интегрирование - широкое поле для деятельности Шерлоков Холмсов от физики. Да и в экономике многие понятия представляются через функции и их производные и поэтому, например, можно по производительности труда в определённый момент времени (производной) восстановить объём продукции, выпущенный в соответствующее время.
Чтобы найти неопределённый интеграл, требуется довольно небольшое количество основных формул интегрирования. Но процесс его нахождения значительно труднее, чем одно лишь применение этих формул. Вся сложность относится не к интегрированию, а к приведению интегрируемого выражения к такому виду, который даёт возможность найти неопределённый интеграл по упомянутым выше основным формулам. Это означает, что для начала практики интегрирования нужно активизировать полученные в средней школе навыки преобразования выражений.
Учиться находить интегралы будем, пользуясь свойствами и таблицей неопределённых интегралов из урока об основных понятиях этой темы (откроется в новом окне).
Существует несколько методов нахождения интеграла, из которых метод замены переменной и метод интегрирования по частям - обязательный джентльменский набор каждого, кто успешно сдал высшую математику. Однако начинать осваивать интегрирование полезнее и приятнее с применением метода разложения, основанном на следующих двух теоремах о свойствах неопределённого интеграла, которые для удобства повторим здесь.
Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
 (2)
(2)
Кроме того, в интегрировании может пригодиться следующее правило: если выражение подынтегральной функции содержит постоянный множитель, то выражение первообразной домножается на число, обратное постоянному множителю, то есть
![]() (3)
(3)
Поскольку этот урок - вводный в решение задач интегрирования, важно отметить две вещи, которые либо уже на самом начальном этапе, либо несколько позже могут вас удивить. Удивление связано с тем фактом, что интегрирование - операция обратная дифференцированию и неопределённый интеграл можно справедливо называть "антипроизводной".
Первая вещь, которой не следует удивляться при интегрировании. В таблице интегралов существуют формулы, которые не имеют аналогов среди формул таблицы производной . Это следующие формулы:
![]()
![]()
Однако можно убедиться в том, что производные выражений, стоящих в правых частях этих формул, совпадают с соответствующими подынтегральными функциями.
Вторая вещь, которой не следует удивляться при интегрировании . Хотя производная любой элементарной функции представляет собой также элементарную функцию, неопределённые интегралы от некоторых элементарных функций уже не являются элементарными функциями . Примерами таких интегралов могут быть следующие:
![]()
![]()
![]()
Для выработки техники интегрирования пригодятся следующие навыки: сокращение дробей, деление многочлена в числителе дроби на одночлен в знаменателе (для получения суммы неопределённых интегралов), преобразование корней в степени, умножение одночлена на многочлен, возведение в степень. Эти навыки нужны для преобразований подынтегрального выражения, в результате которых должна получиться сумма интегралов, присутствующих в таблице интегралов.
Находим неопределённые интегралы вместе
Пример 1. Найти неопределённый интеграл
![]() .
.
Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл 21 (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:
Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:
![]() .
.
Пример 2. Найти неопределённый интеграл
Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:
Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:
![]() .
.
Сокращаем получившиеся дроби и перед нами конечный ответ:
Пример 3. Найти неопределённый интеграл
![]()
Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:
Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда

![]()
объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.
Пример 4. Найти неопределённый интеграл
Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:
![]() .
.
Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:

Продолжаем находить неопределённые интегралы вместе
Пример 7. Найти неопределённый интеграл
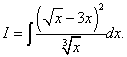
Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов.
Процесс решения интегралов в науке под названием "математика" называется интегрированием. С помощью интегрирования можно находить некоторые физические величины: площадь, объем, массу тел и многое другое.
Интегралы бывают неопределенными и определенными. Рассмотрим вид определенного интеграла и попытаемся понять его физический смысл. Представляется он в таком виде: $$ \int ^a _b f(x) dx $$. Отличительная черта написание определенного интеграла от неопределенного в том, что есть пределы интегрирования a и b. Сейчас узнаем для чего они нужны, и что всё-таки значит определенный интеграл. В геометрическом смысле такой интеграл равен площади фигуры, ограниченной кривой f(x), линиями a и b, и осью Ох.
Из рис.1 видно, что определенный интеграл - это и есть та самая площадь, что закрашена серым цветом. Давайте, проверим это на простейшем примере. Найдем площадь фигуры на изображении представленном ниже с помощью интегрирования, а затем вычислим её обычным способом умножения длины на ширину.

Из рис.2 видно, что $ y=f(x)=3 $, $ a=1, b=2 $. Теперь подставим их в определение интеграла, получаем, что $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2=(3 \cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text{ед}^2 $$ Сделаем проверку обычным способом. В нашем случае длина = 3, ширина фигуры = 1. $$ S = \text{длина} \cdot \text{ширина} = 3 \cdot 1 = 3 \text{ед}^2 $$ Как видим, всё отлично совпало.
Появляется вопрос: как решать интегралы неопределенные и какой у них смысл? Решение таких интегралов - это нахождение первообразных функций. Этот процесс противоположный нахождению производной. Для того, чтобы найти первообразную можно использовать нашу помощь в решении задач по математике или же необходимо самостоятельно безошибочно вызубрить свойства интегралов и таблицу интегрирования простейших элементарных функций. Нахождение выглядит так $$ \int f(x) dx = F(x) + C \text{где} F(x) $ - первообразная $ f(x), C = const $.
Для решения интеграла нужно интегрировать функцию $ f(x) $ по переменной. Если функция табличная, то записывается ответ в подходящем виде. Если же нет, то процесс сводится к получению табличной функции из функции $ f(x) $ путем хитрых математических преобразований. Для этого есть различные методы и свойства, которые рассмотрим далее.
Итак, теперь составим алгоритм как решать интегралы для чайников?
Алгоритм вычисления интегралов
- Узнаем определенный интеграл или нет.
- Если неопределенный, то нужно найти первообразную функцию $ F(x) $ от подынтегральной $ f(x) $ с помощью математических преобразований приводящих к табличному виду функцию $ f(x) $.
- Если определенный, то нужно выполнить шаг 2, а затем подставить пределы $ а $ и $ b $ в первообразную функцию $ F(x) $. По какой формуле это сделать узнаете в статье "Формула Ньютона Лейбница".
Примеры решений
Итак, вы узнали как решать интегралы для чайников, примеры решения интегралов разобрали по полочкам. Узнали физический и геометрический их смысл. О методах решения будет изложено в других статьях.
Решение интегралов - задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл... Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы? Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать интегралы и почему без этого никак нельзя обойтись.
Изучаем понятие "интеграл"
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась. Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Именно эти фундаментальные сведения о Вы найдете у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x) .
Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями:

Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции. Как найти площадь фигуры, ограниченной графиком функции?

С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.
 Бари Алибасов и группа "Интеграл"
Бари Алибасов и группа "Интеграл"
Кстати! Для наших читателей сейчас действует скидка 10% на
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решать неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:

- Константу можно выносить из-под знака интеграла:

- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Линейность:

- Знак интеграла изменяется, если поменять местами пределы интегрирования:

- При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл - это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов
Ниже рассмотрим несколько примеров нахождения неопределенных интегралов. Предлагаем Вам самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Спросите , и они расскажут вам о вычислении интегралов все, что знают сами. С нашей помощью любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
А можно ли под знак дифференциала подводить нелинейную функцию? Да, если подынтегральное выражение представляет собой произведение двух множителей: один множитель — сложная функция от какой-то нелинейной функции, а другой множитель есть производная от этой нелинейной функции. Рассмотрим сказанное на примерах.
Найти неопределенные интегралы.
Пример 1 . ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6 + C.
Что представляет собой данное подынтегральное выражение? Произведение степенной функции от (х 2 + х + 2) и множителя (2х + 1), который равен производной от основания степени: (х 2 + х + 2)" = 2х + 1.
Это и позволило нам подвести (2х + 1) под знак дифференциала:
∫u 5 du=u 6 : 6+ C. (Формула 1). )
Проверка. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)′=1/6 · 6 (x 2 + x + 2) 5 · (x 2 + x + 2)" =
=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1)(x 2 + x + 2) 5 = f (x).
Пример 2. ∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =
=(x³- x²+3x+1) 6 : 6 + C
И чем этот пример отличается от примера 1? Да ничем! Та же пятая степень с основанием (х 3 – х 2 + 3х + 1) умножается на трехчлен (3х 2 – 2х + 3), который является производной основания степени: (х 3 – х 2 + 3х + 1)" = 3х 2 – 2х + 3. Это основание степени мы и подвели под знак дифференциала, от чего значение подынтегрального выражения не изменилось, а затем применили ту же формулу 1). (Интегралы )
Пример 3.
Здесь производная от (2х 3 – 3х) даст (6х 2 – 3), а у нас
имеется (12х 2 – 6), то есть выражение в 2 раза большее, значит, подведем (2х 3 – 3х) под знак дифференциала, а перед интегралом поставим множитель 2 . Применим формулу 2) (лист ).
Вот что получится:

Сделаем проверку, учитывая, что:
Примеры. Найти неопределенные интегралы.
1. ∫(6х+5) 3 dx. Как будем решать? Смотрим в лист и рассуждаем примерно так: подынтегральная функция представляет собой степень, а у нас есть формула для интеграла степени (формула 1) ), но в ней основание степени u и переменная интегрирования тоже u.
А у нас переменная интегрирования х , а основание степени (6х+5) . Сделаем замену переменной интегрирования: вместо dx запишем d (6х+5). Что изменилось? Так как, то, что стоит после знака дифференциала d, по умолчанию, дифференцируется,
то d (6x+5)=6dx, т.е. при замене переменной х на переменную (6х+5) подынтегральная функция возросла в 6 раз, поэтому перед знаком интеграла ставим множитель 1/6. Записать эти рассуждения можно так:
Итак, мы решили этот пример введением новой переменной (переменную х заменили на переменную 6х+5). А куда записали новую переменную (6х+5)? Под знак дифференциала. Поэтому, данный метод введения новой переменной часто называют методом (или способом) подведения (новой переменной) под знак дифференциала .
Во втором примере мы вначале получили степень с отрицательным показателем, а затем подвели под знак дифференциала (7х-2) и использовали формулу интеграла степени 1) (Интегралы ).
Разберем решение примера 3.
Перед интегралом стоит коэффициент 1/5. Почему? Так как d (5x-2)=5dx, то, подведя под знак дифференциала функцию u=5x-2, мы увеличили подынтегральное выражение в 5 раз, поэтому, чтобы значение данного выражения не изменилось — надо было разделить на 5, т.е. умножить на 1/5. Далее, была использована формула 2) (Интегралы) .
Все простейшие формулы интегралов будут иметь вид:
∫f (x) dx=F (x)+C , причем, должно выполняться равенство:
(F (x)+C)"=f (x).
Формулы интегрирования можно получить обращением соответствующих формул дифференцирования.
Действительно,
Показатель степени n может быть и дробным. Часто приходится находить неопределенный интеграл от функции у=√х. Вычислим интеграл от функции f (x)=√x, используя формулу 1) .
Запишем этот пример в виде формулы 2) .
![]()
Так как (х+С)"=1, то ∫dx=x+C.
3) ∫dx=x+C.
Заменяя 1/х² на х -2 , вычислим интеграл от 1/х².
А можно было получить этот ответ обращением известной формулы дифференцирования:
Запишем наши рассуждения в виде формулы 4).
Умножив обе части полученного равенства на 2, получим формулу 5).
Найдем интегралы от основных тригонометрических функций, зная их производные: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Получаем формулы интегрирования 6) — 9).
6) ∫cosxdx=sinx+C;
7) ∫sinxdx=-cosx+C;
После изучения показательной и логарифмической функций, добавим еще несколько формул.
Основные свойства неопределенного интеграла.
I. Производная неопределенного интеграла равна подынтегральной функции.
(∫f (x) dx)"=f (x).
II. Дифференциал неопределенного интеграла равен подынтегральному выражению.
d∫f (x) dx=f (x) dx.
III. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С.
∫dF (x)=F (x)+C или ∫F"(x) dx=F (x)+C.
Обратите внимание: в I, II и III свойствах знаки дифференциала и интеграла (интеграла и дифференциала) «съедают» друг друга!
IV. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла.
∫kf (x) dx=k·∫f (x) dx, где k - постоянная величина, не равная нулю.
V. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.
∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.
VI. Если F (x) есть первообразная для f (x), а k и b — постоянные величины, причем, k ≠0, то (1/k)·F (kx+b) есть первообразная для f (kx+b). Действительно, по правилу вычисления производной сложной функции имеем:
Можно записать:
![]()
Для каждого математического действия существует обратное ему действие. Для действия дифференцирования (нахождения производных функций) тоже существует обратное действие — интегрирование. Посредством интегрирования находят (восстанавливают) функцию по заданной ее производной или дифференциалу. Найденную функцию называют первообразной .
Определение. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство: F′(x)=f (x) .
Примеры. Найти первообразные для функций: 1) f (x)=2x; 2) f (x)=3cos3x.
1) Так как (х²)′=2х, то, по определению, функция F (x)=x² будет являться первообразной для функции f (x)=2x.
2) (sin3x)′=3cos3x. Если обозначить f (x)=3cos3x и F (x)=sin3x, то, по определению первообразной, имеем: F′(x)=f (x), и, значит, F (x)=sin3x является первообразной для f (x)=3cos3x.
Заметим, что и (sin3x+5 )′=3cos3x , и (sin3x-8,2 )′=3cos3x , ... в общем виде можно записать: (sin3x+С )′=3cos3x , где С — некоторая постоянная величина. Эти примеры говорят о неоднозначности действия интегрирования, в отличие от действия дифференцирования, когда у любой дифференцируемой функции существует единственная производная.
Определение. Если функция F (x) является первообразной для функции f (x) на некотором промежутке, то множество всех первообразных этой функции имеет вид:
F (x)+C , где С — любое действительное число.
Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом ∫ (знак интеграла). Записывают: ∫f (x) dx=F (x)+C .
Выражение ∫f (x) dx читают: «интеграл эф от икс по дэ икс».
f (x) dx — подынтегральное выражение,
f (x) — подынтегральная функция,
х — переменная интегрирования.
F (x) — первообразная для функции f (x) ,
С — некоторая постоянная величина.
Теперь рассмотренные примеры можно записать так:
1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.
Что же означает знак d?
d — знак дифференциала — имеет двойное назначение: во-первых, этот знак отделяет подынтегральную функцию от переменной интегрирования; во-вторых, все, что стоит после этого знака диференцируется по умолчанию и умножается на подынтегральную функцию.
Примеры. Найти интегралы: 3) ∫ 2pxdx; 4) ∫ 2pxdp.
3) После значка дифференциала d стоит х х , а р
∫ 2хрdx=рх²+С. Сравните с примером 1).
Сделаем проверку. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).
4) После значка дифференциала d стоит р . Значит, переменная интегрирования р , а множитель х следует считать некоторой постоянной величиной.
∫ 2хрdр=р²х+С. Сравните с примерами 1) и 3).
Сделаем проверку. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).
Страница 1 из 1 1
Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций.
Первообразная и неопределенный интеграл
Первообразная F(x)
от функции f(x)
- это такая функция, производная которой равна f(x)
:
F′(x) = f(x), x ∈ Δ
,
где Δ
- промежуток, на котором выполняется данное уравнение.
Совокупность всех первообразных называется неопределенным интегралом:
,
где C
- постоянная, не зависящая от переменной x
.
Основные формулы и методы интегрирования
Таблица интегралов
Конечная цель вычисления неопределенных интегралов - путем преобразований, привести заданный интеграл к выражению, содержащему простейшие или табличные интегралы.
См. Таблица интегралов >>>
Правило интегрирования суммы (разности)
Вынесение постоянной за знак интеграла
Пусть c - постоянная, не зависящая от x . Тогда ее можно вынести за знак интеграла:
Замена переменной
Пусть x
- функция от переменной t
,
x = φ(t)
,
тогда
.
Или наоборот, t = φ(x)
,
.
С помощью замены переменной можно не только вычислить простые интегралы, но и упростить вычисление более сложных.
Правило интегрирования по частям
Интегрирование дробей (рациональных функций)
Введем обозначение. Пусть P k (x), Q m (x), R n (x) обозначают многочлены степеней k, m, n , соответственно, относительно переменной x .
Рассмотрим интеграл, состоящий из дроби многочленов (так называемая рациональная функция):
Если k ≥ n
,
то сначала нужно выделить целую часть дроби:
.
Интеграл от многочлена S k-n (x)
вычисляется по таблице интегралов.
Остается интеграл:
, где m < n
.
Для его вычисления, подынтегральное выражение нужно разложить на простейшие дроби.
Для этого нужно найти корни уравнения:
Q n (x) = 0
.
Используя полученные корни, нужно представить знаменатель в виде произведения сомножителей:
Q n (x) = s (x-a) n a (x-b) n b ...
(x 2 +ex+f) n e (x 2 +gx+k) n g ...
.
Здесь s
- коэффициент при x n
,
x 2 + ex + f > 0
,
x 2 + gx + k > 0
,
... .
После этого разложить дробь на простейшие:
Интегрируя, получаем выражение, состоящее из более простых интегралов.
Интегралы вида
приводятся к табличным подстановкой t = x - a
.
Рассмотрим интеграл:
Преобразуем числитель:
.
Подставляя в подынтегральное выражение, получаем выражение, в которое входят два интеграла:
,
.
Первый, подстановкой t = x 2 + ex + f
приводится к табличному.
Второй, по формуле приведения:
приводится к интегралу
Приведем его знаменатель к сумме квадратов:
.
Тогда подстановкой , интеграл
также приводится к табличному.
Интегрирование иррациональных функций
Введем обозначение. Пусть R(u 1 , u 2 , ... , u n)
означает рациональную функцию от переменных u 1 , u 2 , ... , u n
.
То есть
,
где P, Q
- многочлены от переменных u 1 , u 2 , ... , u n
.
Дробно-линейная иррациональность
Рассмотрим интегралы вида:
,
где - рациональные числа, m 1 , n 1 , ..., m s , n s
- целые числа.
Пусть n
- общий знаменатель чисел r 1 , ..., r s
.
Тогда интеграл сводится к интегралу от рациональных функций подстановкой:
.
Интегралы от дифференциальных биномов
Рассмотрим интеграл:
,
где m, n, p
- рациональные числа, a, b
- действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.
1)
Если p
- целое. Подстановка x = t N
,
где N
- общий знаменатель дробей m
и n
.
2)
Если - целое. Подстановка a x n + b = t M
,
где M
- знаменатель числа p
.
3)
Если - целое. Подстановка a + b x - n = t M
,
где M
- знаменатель числа p
.
Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.
В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям m
и p
.
Это можно сделать с помощью формул приведения:
;
.
Интегралы, содержащие квадратный корень из квадратного трехчлена
Здесь мы рассматриваем интегралы вида:
,
Подстановки Эйлера
Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0
;
, при c > 0
;
, где x 1
- корень уравнения a x 2 + b x + c = 0
.
Если это уравнение имеет действительные корни.
Тригонометрические и гиперболические подстановки
Прямые методы
В большинстве случаев, подстановки Эйлера приводят к более длинным вычислениям, чем прямые методы. С помощью прямых методов интеграл приводится к одному из перечисленных ниже видов.
I тип
Интеграл вида:
,
где P n (x)
- многочлен степени n
.
Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:
Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты A i
.
II тип
Интеграл вида:
,
где P m (x)
- многочлен степени m
.
Подстановкой t = (x - α) -1 этот интеграл приводится к предыдущему типу. Если m ≥ n , то у дроби следует выделить целую часть.
III тип
Третий и наиболее сложный тип:
.
Здесь нужно сделать подстановку:
.
После чего интеграл примет вид:
.
Далее, постоянные α, β
нужно выбрать такими, чтобы коэффициенты при t
обратились в нуль:
B = 0, B 1 = 0
.
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
z 2 = A 1 t 2 + C 1
;
y 2 = A 1 + C 1 t -2
.
Общий случай
Интегрирование трансцендентных (тригонометрических и показательных) функций
Заранее отметим, что те методы, которые применимы для тригонометрических функций, также применимы и для гиперболических функций. По этой причине мы не будем рассматривать интегрирование гиперболических функций отдельно.
Интегрирование рациональных тригонометрических функций от cos x и sin x
Рассмотрим интегралы от тригонометрических функций вида:
,
где R
- рациональная функция. Сюда также могут входить тангенсы и котангенсы, которые следует преобразовать через синусы и косинусы.
При интегрировании таких функций полезно иметь в виду три правила:
1)
если R(cos
x, sin
x)
умножается на -1
от перемены знака перед одной из величин cos
x
или sin
x
,
то полезно другую из них обозначить через t
.
2)
если R(cos
x, sin
x)
не меняется от перемены знака одновременно перед cos
x
и sin
x
,
то полезно положить tg
x = t
или ctg
x = t
.
3)
подстановка во всех случаях приводит к интегралу от рациональной дроби. К сожалению, эта подстановка приводит к более длинным вычислениям чем предыдущие, если они применимы.
Произведение степенных функций от cos x и sin x
Рассмотрим интегралы вида:
Если m и n - рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.
Если m и n - целые числа, то интегралы вычисляются интегрированием по частям. При этом получаются следующие формулы приведения:
;
;
;
.
Интегрирование по частям
Применение формулы Эйлера
Если подынтегральное выражение линейно относительно одной из функций
cos
ax
или sin
ax
,
то удобно применить формулу Эйлера:
e iax = cos
ax + isin
ax
(где i 2 = -1
),
заменив эту функцию на e
iax
и выделив действительную (при замене cos
ax
) или мнимую часть (при замене sin
ax
) из полученного результата.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
